Wideo: Jaki jest wzór Eulera wykorzystujący liczbę ścian czworościanu o wierzchołkach jako 4 i 6 krawędziach?
2024 Autor: Stanley Ellington | [email protected]. Ostatnio zmodyfikowany: 2023-12-16 00:21
Ta strona zawiera listę dowodów Wzór Eulera : dla dowolny wielościan wypukły, numer z wierzchołki oraz twarze razem to dokładnie dwa więcej niż numer z krawędzie . Symbolicznie V−E+F=2. Do przykład, a czworościan ma cztery wierzchołki , cztery twarze i sześć krawędzie ; 4 - 6 + 4 =2.
W konsekwencji, jaka będzie liczba ścian, jeśli będzie 6 wierzchołków i 12 krawędzi?
Sześcian lub prostopadłościan to trójwymiarowy kształt, który ma 12 krawędzi , 8 rogi lub wierzchołki , oraz 6 twarzy.
Można też zapytać, jak działa formuła Eulera? Wzór Eulera , jedno z dwóch ważnych twierdzeń matematycznych Leonharda Euler . Pierwsza to topologiczna niezmienność (patrz topologia) odnosząca się do liczby ścian, wierzchołków i krawędzi dowolnego wielościanu. Jest napisane F + V = E + 2, gdzie F jest liczbą ścian, V liczbą wierzchołków, a E liczbą krawędzi.
jaki jest wzór na związek między liczbą wierzchołków ścian a krawędziami sześcianu?
V - E + F = 2; lub słownie: the numer z wierzchołki , bez numer z krawędzie , plus liczba twarzy , jest równy do dwa.
Co to jest wzór wielościanu Eulera?
To twierdzenie obejmuje: Wielościenna formuła Eulera (Czasami nazywany Wzór Eulera ). Dzisiaj wyrazilibyśmy ten wynik jako: Liczba wierzchołków V, ścian F i krawędzi E w wypukłej trójwymiarowej wielościan , spełnij V + F - E = 2.
Zalecana:
Jaki jest wzór empiryczny dla cykloheksanu?
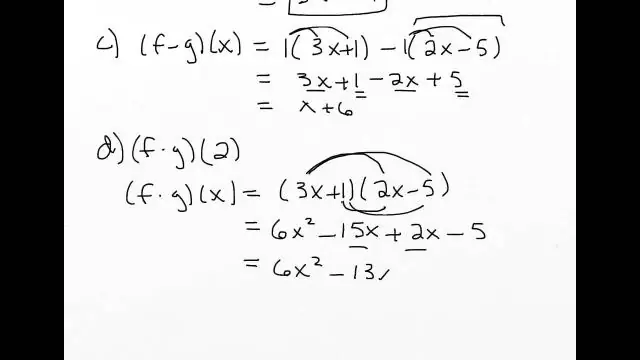
Empiryczny wzór cykloheksanu to CH2, a jego masa cząsteczkowa to 84,16 amu
Jak zapisać 7 3 jako liczbę mieszaną?
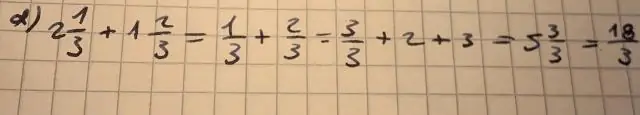
Aby zapisać ułamek 7/3 jako liczbę całkowitą lub mieszaną, dzielimy 7 przez 3, aby otrzymać 2 resztę 1
Jaki jest wzór na elastyczność krzyżową cen?
Elastyczność krzyżowa (Exy) mówi nam o relacji między dwoma produktami. mierzy wrażliwość zmiany popytu ilościowego produktu X na zmianę ceny produktu Y. Formuła elastyczności cenowej: Exy = procentowa zmiana ilości popytu X / procentowa zmiana ceny Y
Jak pomnożyć liczbę mieszaną przez liczbę całkowitą?
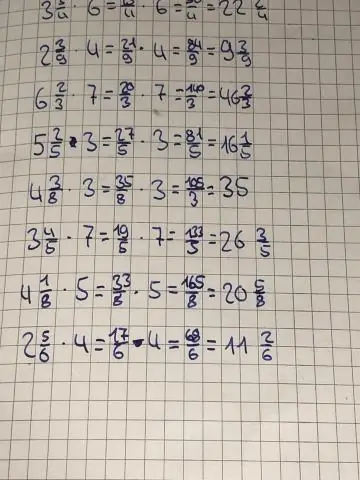
Mnożenie liczby mieszanej i liczby całkowitej Liczbę mieszaną zamieniamy na ułamek niewłaściwy, a liczbę całkowitą zapisujemy jako mianownik ułamkowy. Przeprowadza się mnożenie frakcji i w razie potrzeby dokonuje się uproszczeń. Wynikowy ułamek jest zapisany jako liczba mieszana najprostsza forma
Jaki jest cel ścian?
Przeznaczeniem ścian w budynkach jest podparcie dachów, podłóg i stropów; zamknąć przestrzeń jako część przegród budynku wraz z dachem, aby nadać budynkom formę; oraz zapewnić schronienie i bezpieczeństwo. Dodatkowo na ścianie mogą znajdować się różnego rodzaju media takie jak instalacja elektryczna czy wodno-kanalizacyjna