Wideo: Jak wyrazić powtarzającą się liczbę dziesiętną za pomocą serii nieskończonej?
2024 Autor: Stanley Ellington | [email protected]. Ostatnio zmodyfikowany: 2023-12-16 00:21
A powtarzanie dziesiętne jest dziesiętny czyje cyfry powtarzać . jakiś nieskończony geometryczny seria jest seria liczb, które ciągną się w nieskończoność, które mają ten sam stały stosunek między wszystkimi kolejnymi liczbami. Wszystko powtarzanie ułamków dziesiętnych można przepisać jako nieskończony geometryczny seria tej postaci: a + ar + ar2 + ar3 + …
Skąd wiesz, kiedy ułamek dziesiętny się powtarza?
Wystarczy podzielić licznik przez mianownik. Jeśli skończysz z resztą 0, oznacza to zakończenie dziesiętny . W przeciwnym razie resztki zaczną się powtarzać po pewnym czasie i masz powtarzanie dziesiętne.
Podobnie, 0,25 kończy się czy powtarza? Na przykład 1/4 to mniej niż jeden, podobnie jak 2500/9999. Liczbą dziesiętną dla tych ułamków będzie albo a zakończenie dziesiętny lub a powtórzenie dziesiętny. Jeśli podzielimy 1 przez 4, otrzymamy 0.25 a następnie tyle zer, ile chcemy. To jest zakończenie liczba dziesiętna.
Aby wiedzieć, co umieszczasz nad powtarzalnym dziesiętnym?
Powtarzające się ułamki dziesiętne to liczby, które są kontynuowane po dziesiętny , na przykład 0,356(356). Zwykle pisze się poziomą linię, zwaną vinculum nad ten powtórzenie wzór cyfr. Najłatwiejszy i najbardziej precyzyjny sposób na dodaj powtarzające się ułamki dziesiętne jest włączenie dziesiętny na ułamek.
Co to jest 0,123 powtórzenia jako ułamek?
Najpierw niech 0.123 (123 powtarzane) będzie x. Ponieważ x to powtarzające się w 3 miejscach po przecinku mnożymy przez 1000. Następnie odejmujemy je. Na koniec dzielimy obie strony przez 999, aby otrzymać x jako a frakcja.
Zalecana:
Jak znaleźć minimalną liczbę stacji roboczych?
Oblicz teoretyczną minimalną liczbę stanowisk roboczych. LICZBA STANOWISK PRACY = (SUMA CAŁKOWITYCH CZASU ZADAŃ) / (CZAS CYKLU)= 70 min / 15 min = 4,67 &asym;5 (zaokrąglone) Liczba zadań Następujące zadania KROK 4
Jak zracjonalizować licznik za pomocą dwóch terminów?
Krok 1: Aby zracjonalizować mianownik, musisz pomnożyć zarówno licznik, jak i mianownik przez sprzężenie mianownika. Pamiętaj, aby znaleźć koniugat, wszystko, co musisz zrobić, to zmienić znak między tymi dwoma terminami. Krok 2: Rozłóż (lub FOIL) zarówno licznik, jak i mianownik
Ile godzin powinieneś uczyć się do serii 63?
Seria 63 - NASAA Uniform Securities Agent State Law Exam. Zalecamy naukę 30-40 godzin przez dziesięć dni
Czy gość może wyrazić zgodę policji na przeszukanie?
Jeśli policja nie ma nakazu, prawdopodobnie nie może przeszukać domu na mocy Czwartej Poprawki, chyba że ma zastosowanie wyjątek. Tymczasem gość może wyrazić ważną zgodę na przeszukanie kontrolowanych przez siebie obszarów, nawet jeśli nie mieszka w domu
Jak pomnożyć liczbę mieszaną przez liczbę całkowitą?
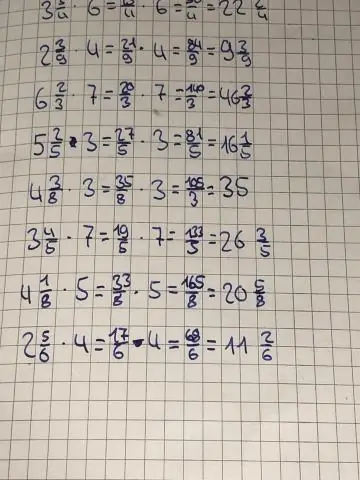
Mnożenie liczby mieszanej i liczby całkowitej Liczbę mieszaną zamieniamy na ułamek niewłaściwy, a liczbę całkowitą zapisujemy jako mianownik ułamkowy. Przeprowadza się mnożenie frakcji i w razie potrzeby dokonuje się uproszczeń. Wynikowy ułamek jest zapisany jako liczba mieszana najprostsza forma